The Computational Expressiveness of a Model Train Set: A Paperlet

My son Daniel had his fourth birthday a couple weeks ago. For a present, he got an electric train set. (For completeness—and since the details of the train set will be rather important to the post—it’s called “WESPREX Create a Dinosaur Track”, but this is not an ad and I’m not getting a kickback for it.)

As you can see, the main feature of this set is a Y-shaped junction, which has a flap that can control which direction the train goes. The logic is as follows:

• If the train is coming up from the “bottom” of the Y, then it continues to either the left arm or the right arm, depending on where the flap is. It leaves the flap as it was.

• If the train is coming down the left or right arms of the Y, then it continues to the bottom of the Y, pushing the flap out of its way if it’s in the way. (Thus, if the train were ever to return to this Y-junction coming up from the bottom, not having passed the junction in the interim, it would necessarily go to the same arm, left or right, that it came down from.)

The train set also comes with bridges and tunnels; thus, there’s no restriction of planarity. Finally, the train set comes with little gadgets that can reverse the train’s direction, sending it back in the direction that it came from:

These gadgets don’t seem particularly important, though, since we could always replace them if we wanted by a Y-junction together with a loop.

Notice that, at each Y-junction, the position of the flap stores one bit of internal state, and that the train can both “read” and “write” these bits as it moves around. Thus, a question naturally arises: can this train set do any nontrivial computations? If there are n Y-junctions, then can it cycle through exp(n) different states? Could it even solve PSPACE-complete problems, if we let it run for exponential time? (For a very different example of a model-train-like system that, as it turns out, is able to express PSPACE-complete problems, see this recent paper by Erik Demaine et al.)

Whatever the answers regarding Daniel’s train set, I knew immediately on watching the thing go that I’d have to write a “paperlet” on the problem and publish it on my blog (no, I don’t inflict such things on journals!). Today’s post constitutes my third “paperlet,” on the general theme of a discrete dynamical system that someone showed me in real life (e.g. in a children’s toy or in biology) having more structure and regularity than one might naïvely expect. My first such paperlet, from 2014, was on a 1960s toy called the Digi-Comp II; my second, from 2016, was on DNA strings acted on by recombinase (OK, that one was associated with a paper in Science, but my combinatorial analysis wasn’t the main point of the paper).

Anyway, after spending an enjoyable evening on the problem of Daniel’s train set, I was able to prove that, alas, the possible behaviors are quite limited (I classified them all), falling far short of computational universality.

If you feel like I’m wasting your time with trivialities (or if you simply enjoy puzzles), then before you read any further, I encourage you to stop and try to prove this for yourself!

Back yet? OK then…

Theorem: Assume a finite amount of train track. Then after a linear amount of time, the train will necessarily enter a “boring infinite loop”—i.e., an attractor state in which at most two of the flaps keep getting toggled, and the rest of the flaps are fixed in place. In more detail, the attractor must take one of four forms:

I. a line (with reversing gadgets on both ends),
II. a simple cycle,
III. a “lollipop” (with one reversing gadget and one flap that keeps getting toggled), or
IV. a “dumbbell” (with two flaps that keep getting toggled).

In more detail still, there are seven possible topologically distinct trajectories for the train, as shown in the figure below.

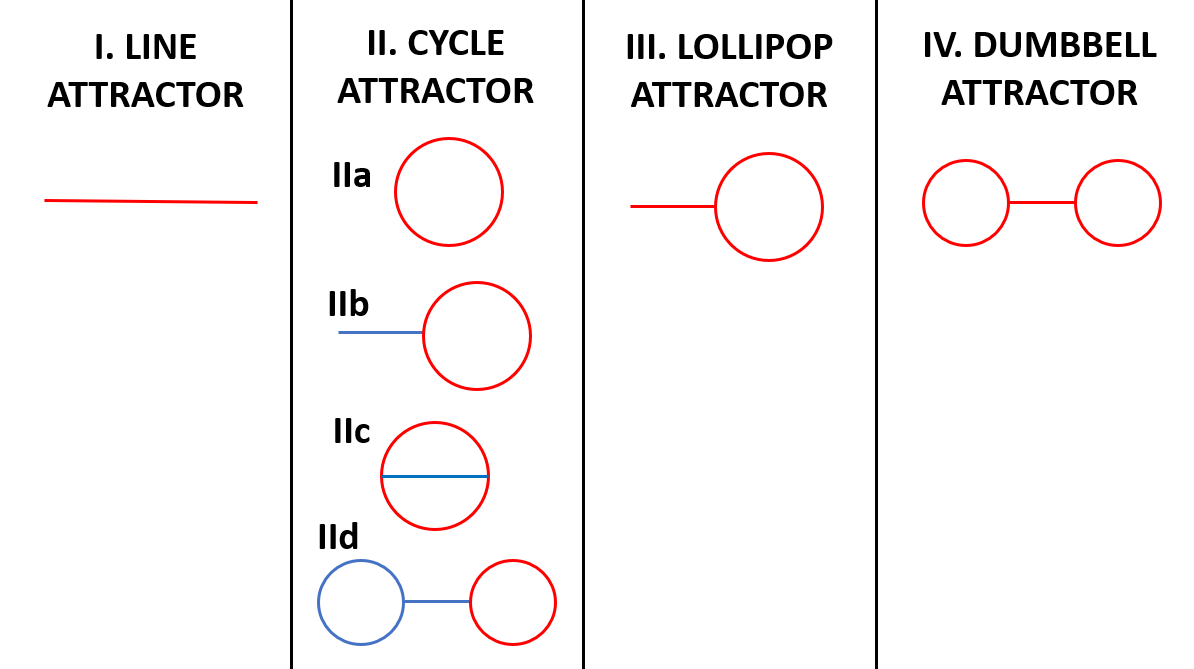
Here the red paths represent the attractors, where the train loops around and around for an unlimited amount of time, while the blue paths represent “runways” where the train spends a limited amount of time on its way into the attractor. Every degree-3 vertex is assumed to have a Y-junction, while every degree-1 vertex is assumed to have a reversing gadget, unless (in IIb) the train starts at that vertex and never returns to it.

The proof of the theorem rests on two simple observations.

Observation 1: While the Y-junctions correspond to vertices of degree 3, there are no vertices of degree 4 or higher. This means that, if the train ever revisits a vertex v (other than the start vertex) for a second time, then there must be some edge e incident to v that it also traverses for a second time immediately afterward.

Observation 2: Suppose the train traverses some edge e, then goes around a simple cycle (meaning, one where no edges or vertices are reused), and then traverses e again, going in the same direction as the first time. Then from that point forward, the train will just continue around the same simple cycle forever.

The proof of Observation 2 is simply that, if there were any flap that might be in the train’s way as it continued around the simple cycle, then the train would already have pushed it out of the way its first time around the cycle, and nothing that happened thereafter could possibly change the flap’s position.

Using the two observations above, let’s now prove the theorem. Let the train start where it will, and follow it as it traces out a path. Since the graph is finite, at some point some already-traversed edge must be traversed a second time. Let e be the first such edge. By Observation 1, this will also be the first time the train’s path intersects itself at all. There are then three cases:

Case 1: The train traverses e in the same direction as it did the first time. By Observation 2, the train is now stuck in a simple cycle forever after. So the only question is what the train could’ve done before entering the simple cycle. We claim that at most, it could’ve traversed a simple path. For otherwise, we’d contradict the assumption that e was the first edge that the train visited twice on its journey. So the trajectory must have type IIa, IIb, or IIc in the figure.

Case 2: Immediately after traversing e, the train hits a reversing gadget and traverses e again the other way. In this case, the train will clearly retrace its entire path and then continue past its starting point; the question is what happens next. If it hits another reversing gadget, then the trajectory will have type I in the figure. If it enters a simple cycle and stays in it, then the trajectory will have type IIb in the figure. If, finally, it makes a simple cycle and then exits the cycle, then the trajectory will have type III in the figure. In this last case, the train’s trajectory will form a “lollipop” shape. Note that there must be a Y-junction where the “stick” of the lollipop meets the “candy” (i.e., the simple cycle), with the base of the Y aligned with the stick (since otherwise the train would’ve continued around and around the candy). From this, we deduce that every time the train goes around the candy, it does so in a different orientation (clockwise or counterclockwise) than the time before; and that the train toggles the Y-junction’s flap every time it exits the candy (although not when it enters the candy).

Case 3: At some point after traversing e in the forward direction (but not immediately after), the train traverses e in the reverse direction. In this case, the broad picture is analogous to Case 2. So far, the train has made a lollipop with a Y-junction connecting the stick to the candy (i.e. cycle), the base of the Y aligned with the stick, and e at the very top of the stick. The question is what happens next. If the train next hits a reversing gadget, the trajectory will have type III in the figure. If it enters a new simple cycle, disjoint from the first cycle, and never leaves it, the trajectory will have type IId in the figure. If it enters a new simple cycle, disjoint from the first cycle, and does leave it, then the trajectory now has a “dumbbell” pattern, type IV in the figure (also shown in the first video). There’s only one last situation to worry about: namely, that the train makes a new cycle that intersects the first cycle, forming a “theta” (θ) shaped trajectory. In this case, there must be a Y-junction at the point where the new cycle bumps into the old cycle. Now, if the base of the Y isn’t part of the old cycle, then the train never could’ve made it all the way around the old cycle in the first place (it would’ve exited the old cycle at this Y-junction), contradiction. If the base of the Y is part of the old cycle, then the flap must have been initially set to let the train make it all the way around the old cycle; when the train then reenters the old cycle, the flap must be moved so that the train will never make it all the way around the old cycle again. So now the train is stuck in a new simple cycle (sharing some edges with the old cycle), and the trajectory has type IIc in the figure.

This completes the proof of the theorem.

We might wonder: why isn’t this model train set capable of universal computation, of AND, OR, and NOT gates—or at any rate, of some computation more interesting than repeatedly toggling one or two flaps? My answer might sound tautological: it’s simply that the logic of the Y-junctions is too limited. Yes, the flaps can get pushed out of the way—that’s a “bit flip”—but every time such a flip happens, it helps to set up a “groove” in which the train just wants to continue around and around forever, not flipping any additional bits, with only the minor complications of the lollipop and dumbbell structures to deal with. Even though my proof of the theorem might’ve seemed like a tedious case analysis, it had this as its unifying message.

It’s interesting to think about what gadgets would need to be added to the train set to make it computationally universal, or at least expressively richer—able, as turned out to be the case for the Digi-Comp II, to express some nontrivial complexity class falling short of P. So for example, what if we had degree-4 vertices, with little turnstile gadgets? Or multiple trains, which could be synchronized to the millisecond to control how they interacted with each other via the flaps, or which could even crash into each other? I look forward to reading your ideas in the comment section!

For the truth is this: quantum complexity classes, BosonSampling, closed timelike curves, circuit complexity in black holes and AdS/CFT, etc. etc.—all these topics are great, but the same models and problems do get stale after a while. I aspire for my research agenda to chug forward, full steam ahead, into new computational domains.

PS. Happy Easter to those who celebrate!