ParityQC and University of Innsbruck Introduce SWAP-less, Efficient Quantum Fourier Transform for Limited Connectivity Systems

Insider Brief:

• ParityQC and the University of Innsbruck developed a formalism that efficiently implements the Quantum Fourier Transform (QFT) on linear chains, eliminating the need for SWAP or shuttling operations that traditionally reduce fidelity.

• The Quantum Fourier Transform is a crucial component in algorithms like Shor’s algorithm and quantum optimization techniques, but its implementation on linear chains is challenging due to limited qubit connectivity.

• The researchers’ SWAP-less method improves circuit depth to 5n−3 and reduces gate count to n²−1 CNOT gates, enhancing performance and reducing errors in quantum systems.

• This formalism may significantly influence future quantum algorithm development by optimizing resource use on devices with limited connectivity, supporting scalable quantum computing applications.

PRESS RELEASE — Navigating the challenge of enabling gate operations between qubits in quantum computers is essential for executing quantum circuits. Current quantum devices are limited in their ability to perform operations between all qubits, as qubits cannot be copied or read without information loss, and physical interactions diminish over distance. As a result, alternatives like SWAP operations or shuttling are used to simulate connectivity, but these are computationally expensive and reduce fidelity.

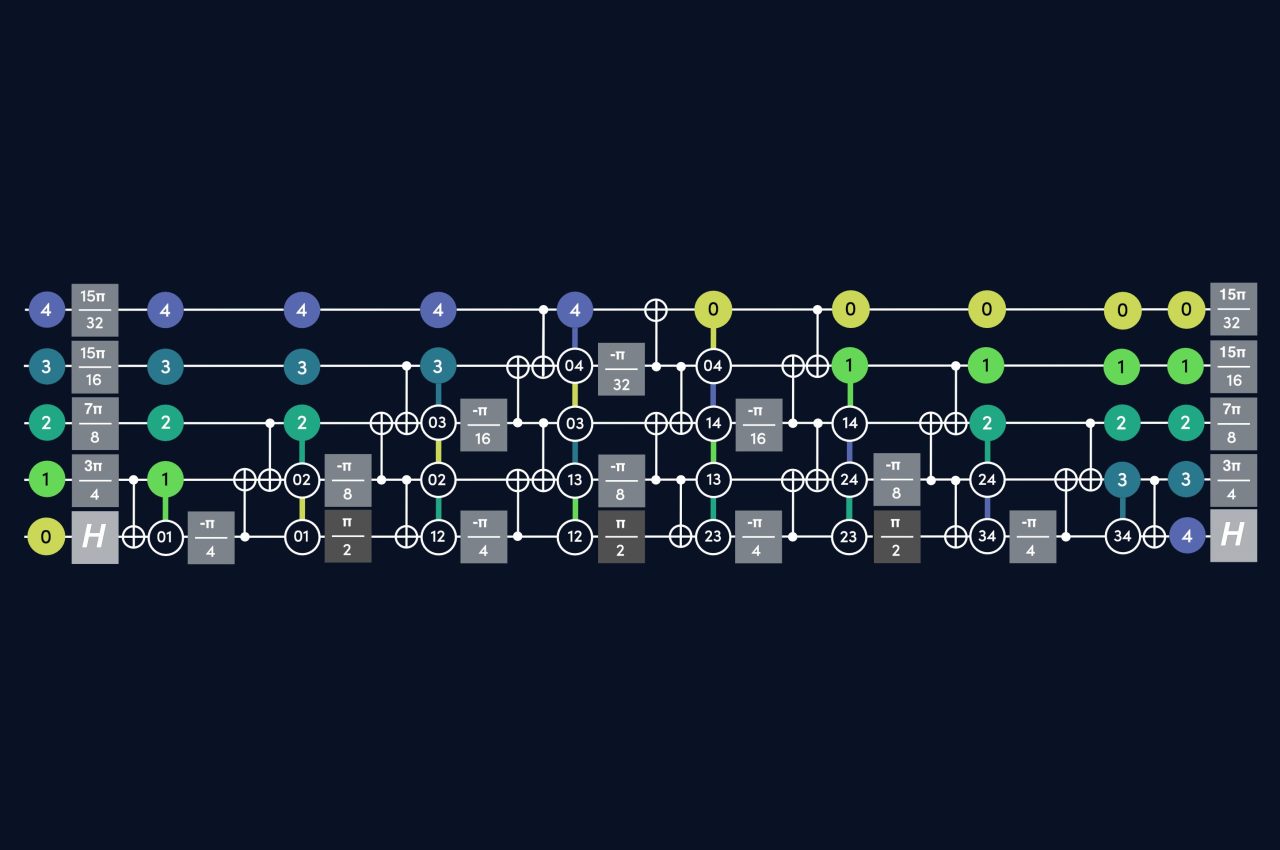
ParityQC and the University of Innsbruck recently announced the formulation of a formalism that can be used in what they describe as “the most efficient implementation of the Quantum Fourier Transform (QFT) on a linear chain” as it eliminates the need for SWAP or shuttling operations traditionally used to transport quantum information. According to the corresponding arXiv preprint, this new approach is specifically designed to optimize resource use on quantum devices with limited connectivity.

The Role and Importance of the Quantum Fourier Transform

As noted in the preprint, the QFT serves as the foundation for algorithms such as Shor’s algorithm. It is also used in various quantum optimization techniques. In practical applications, QFT plays a role in a variety of quantum algorithms that impact fields ranging from cryptography to quantum optimization, making it one of the more studied quantum processes. Its efficiency in implementation is important for enhancing the performance of quantum algorithms, especially on NISQ devices where each additional gate operation increases the likelihood of introducing errors into the system.

However, the QFT requires gate operations between all qubits, which presents a challenge on hardware with limited qubit connectivity, such as linear chains, where each qubit is only connected to its nearest neighbors, forming a sequential line. This is in contrast to all-to-all connectivity where any qubit can interact with any other qubit. Linear chains are often used in hardware architectures such as ion traps and are a common challenge for efficient quantum algorithm implementation due to their restricted interaction pathways.

Implementing the QFT on a linear chain generally requires additional operations to move information across the system, typically handled through SWAP operations or physical shuttling of qubits. These methods, however, introduce overhead and reduce computational fidelity.

According to the researchers, the elimination of these extra steps may provide significant improvements. The press release notes that this SWAP-less method not only avoids the additional overhead but also improves circuit depth and gate efficiency, two central factors in practical quantum computation.

Overcoming Connectivity Constraints with SWAP-less Methods

The ParityQC team implemented QFT on a linear chain and achieved a total circuit depth of 5n−3 and requiring n² −1 CNOT gates, where n is the number of qubits. As stated by the team, these results represent an improvement over the current state-of-the-art implementations, which involve higher gate counts and longer circuit depths. The reduced number of gates and circuit depth both contribute to minimizing the introduction of errors in quantum systems.

Additionally, this new formalism, based on tracking parity quantum information, demonstrates that entangling gates, often used to manipulate quantum states, may also be used to transport quantum information effectively, providing an alternative to SWAP or shuttling operations.

Potential Impact on Quantum Algorithm Design

According to the researchers, this method could have implications for the future of quantum algorithm development, particularly for architectures with limited connectivity, as it provides a more efficient use of resources. The ParityQC Architecture, is noted as gaining attention for its potential to support scalable quantum computing across multiple applications. These results build on the architecture’s foundation and could have influence how quantum algorithms are designed for use on hardware with connectivity constraints.