On black holes, holography, the Quantum Extended Church-Turing Thesis, fully homomorphic encryption, and brain uploading

I promise you: this post is going to tell a scientifically coherent story that involves all five topics listed in the title. Not one can be omitted.

My story starts with a Zoom talk that the one and only Lenny Susskind delivered for the Simons Institute for Theory of Computing back in May. There followed a panel discussion involving Lenny, Edward Witten, Geoffrey Penington, Umesh Vazirani, and your humble shtetlmaster.

Lenny’s talk led up to a gedankenexperiment involving an observer, Alice, who bravely jumps into a specially-prepared black hole, in order to see the answer to a certain computational problem in her final seconds before being ripped to shreds near the singularity. Drawing on earlier work by Bouland, Fefferman, and Vazirani, Lenny speculated that the computational problem could be exponentially hard even for a (standard) quantum computer. Despite this, Lenny repeatedly insisted—indeed, he asked me again to stress here—that he was not claiming to violate the Quantum Extended Church-Turing Thesis (QECTT), the statement that all of nature can be efficiently simulated by a standard quantum computer. Instead, he was simply investigating how the QECTT needs to be formulated in order to be a true statement.

I didn’t understand this, to put it mildly. If what Lenny was saying was right—i.e., if the infalling observer could see the answer to a computational problem not in BQP, or Bounded-Error Quantum Polynomial-Time—then why shouldn’t we call that a violation of the QECTT? Just like we call Shor’s quantum factoring algorithm a likely violation of the classical Extended Church-Turing Thesis, the thesis saying that nature can be efficiently simulated by a classical computer? Granted, you don’t have to die in order to run Shor’s algorithm, as you do to run Lenny’s experiment. But why should such implementation details matter from the lofty heights of computational complexity?

Alas, not only did Lenny never answer that in a way that made sense to me, he kept trying to shift the focus from real, physical black holes to “silicon spheres” made of qubits, which would be programmed to simulate the process of Alice jumping into the black hole (in a dual boundary description). Say what? Granting that Lenny’s silicon spheres, being quantum computers under another name, could clearly be simulated in BQP, wouldn’t this still leave the question about the computational powers of observers who jump into actual black holes—i.e., the question that we presumably cared about in the first place?

Confusing me even further, Witten seemed almost dismissive of the idea that Lenny’s gedankenexperiment raised any new issue for the QECTT—that is, any issue that wouldn’t already have been present in a universe without gravity. But as to Witten’s reasons, the most I understood from his remarks was that he was worried about various “engineering” issues with implementing Lenny’s gedankenexperiment, involving gravitational backreaction and the like. Ed Witten, now suddenly the practical guy! I couldn’t even isolate the crux of disagreement between Susskind and Witten, since after all, they agreed (bizarrely, from my perspective) that the QECTT wasn’t violated. Why wasn’t it?

Anyway, shortly afterward I attended the 28th Solvay Conference in Brussels, where one of the central benefits I got—besides seeing friends after a long COVID absence and eating some amazing chocolate mousse—was a dramatically clearer understanding of the issues in Lenny’s gedankenexperiment. I owe this improved understanding to conversations with many people at Solvay, but above all Daniel Gottesman and Daniel Harlow. Lenny himself wasn’t there, other than in spirit, but I ran the Daniels’ picture by him afterwards and he assented to all of its essentials.

The Daniels’ picture is what I want to explain in this post. Needless to say, I take sole responsibility for any errors in my presentation, as I also take sole responsibility for not understanding (or rather: not doing the work to translate into terms that I understood) what Susskind and Witten had said to me before.

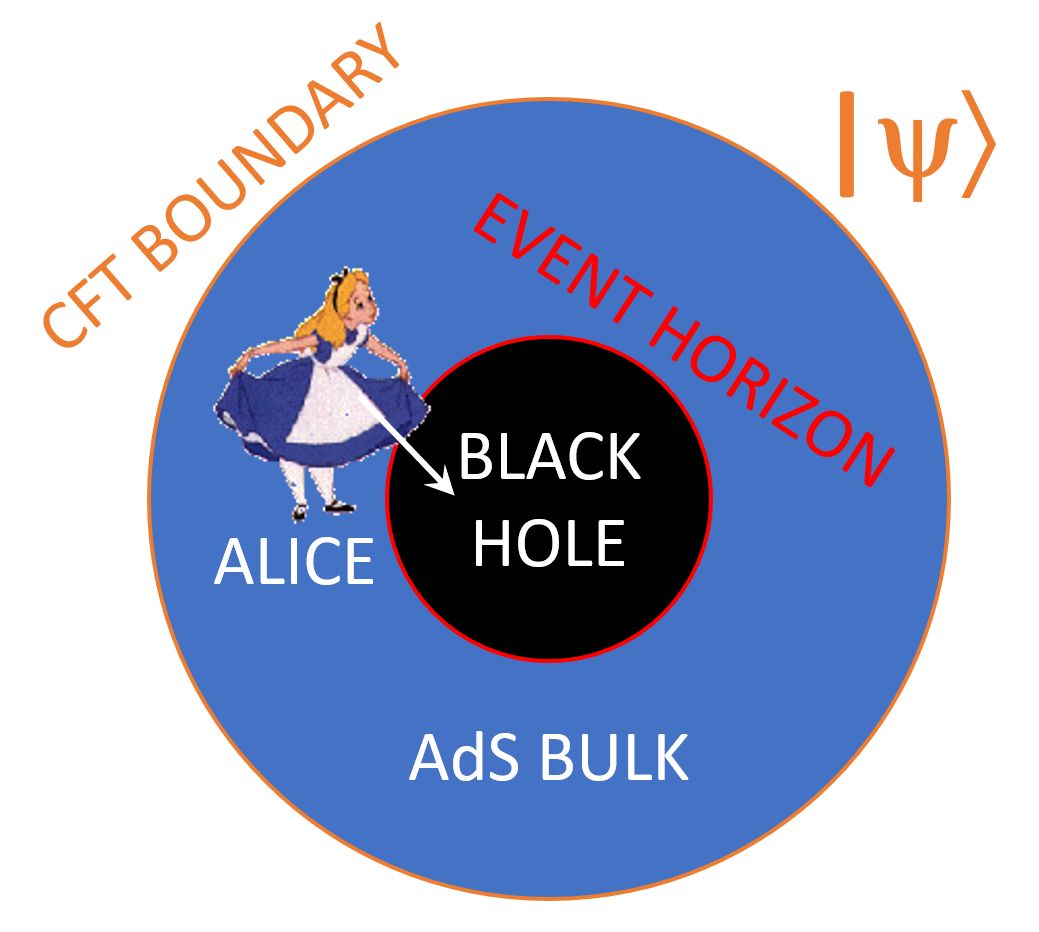
The first thing you need to understand about Lenny’s gedankenexperiment is that it takes place entirely in the context of AdS/CFT: the famous holographic duality between two types of physical theories that look wildly different. Here AdS stands for anti-de-Sitter: a quantum theory of gravity describing a D-dimensional universe with a negative cosmological constant (i.e. hyperbolic geometry), one where black holes can form and evaporate and so forth. Meanwhile, CFT stands for conformal field theory: a quantum field theory, with no apparent gravity (and hence no black holes), that lives on the (D-1)-dimensional boundary of the D-dimensional AdS space. The staggering claim of AdS/CFT is that every physical question about the AdS bulk can be translated into an equivalent question about the CFT boundary, and vice versa, with a one-to-one mapping from states to states and observables to observables. So in that sense, they’re actually the same theory, just viewed in two radically different ways. AdS/CFT originally came out of string theory, but then notoriously “swallowed its parent,” to the point where nowadays, if you go to what are still called “string theory” meetings, you’re liable to hear vastly more discussion of AdS/CFT than of actual strings.

Thankfully, the story I want to tell won’t depend on fine details of how AdS/CFT works. Nevertheless, you can’t just ignore the AdS/CFT part as some technicality, in order to get on with the vivid tale of Alice jumping into a black hole, hoping to learn the answer to a beyond-BQP computational problem in her final seconds of existence. The reason you can’t ignore it is that the whole beyond-BQP computational problem we’ll be talking about, involves the translation (or “dictionary”) between the AdS bulk and the CFT boundary. If you like, then, it’s actually the chasm between bulk and boundary that plays the starring role in this story. The more familiar chasm within the bulk, between the interior of a black hole and its exterior (the two separated by an event horizon), plays only a subsidiary role: that of causing the AdS/CFT dictionary to become exponentially complex, as far as anyone can tell.

Pause for a minute. Previously I led you to believe that we’d be talking about an actual observer Alice, jumping into an actual physical black hole, and whether Alice could see the answer to a problem that’s intractable even for quantum computers in her last moments before hitting the singularity, and if so whether we should take that to refute the Quantum Extended Church-Turing Thesis. What I’m saying now is so wildly at variance with that picture, that it had to be repeated to me about 10 times before I understood it. Once I did understand, I then had to repeat it to others about 10 times before they understood. And I don’t care if people ridicule me for that admission—how slow Scott and his friends must be, compared to string theorists!—because my only goal right now is to get you to understand it.

To say it again: Lenny has not proposed a way for Alice to surpass the complexity-theoretic power of quantum computers, even for a brief moment, by crossing the event horizon of a black hole. If that was Alice’s goal when she jumped into the black hole, then alas, she probably sacrificed her life for nothing! As far as anyone knows, Alice’s experiences, even after crossing the event horizon, ought to continue to be described extremely well by general relativity and quantum field theory (at least until she nears the singularity and dies), and therefore ought to be simulatable in BQP. Granted, we don’t actually know this—you can call it an open problem if you like—but it seems like a reasonable guess.

In that case, though, what beyond-BQP problem was Lenny talking about, and what does it have to do with black holes? Building on the Bouland-Fefferman-Vazirani paper, Lenny was interested in a class of problems of the following form: Alice is given as input a pure quantum state |ψ⟩, which encodes a boundary CFT state, which is dual to an AdS bulk universe that contains a black hole. Alice’s goal is, by examining |ψ⟩, to learn something about what’s inside the black hole. For example: does the black hole interior contain “shockwaves,” and if so how many and what kind? Does it contain a wormhole, connecting it to a different black hole in another universe? If so, what’s the volume of that wormhole? (Not the first question I would ask either, but bear with me.)

Now, when I say Alice is “given” the state |ψ⟩, this could mean several things: she could just be physically given a collection of n qubits. Or, she could be given a gigantic table of 2ⁿ amplitudes. Or, as a third possibility, she could be given a description of a quantum circuit that prepares |ψ⟩, say from the all-0 initial state |0ⁿ⟩. Each of these possibilities leads to a different complexity-theoretic picture, and the differences are extremely interesting to me, so that’s what I mostly focused on in my remarks in the panel discussion after Lenny’s talk. But it won’t matter much for the story I want to tell in this post.

However |ψ⟩ is given to Alice, the prediction of AdS/CFT is that |ψ⟩ encodes everything there is to know about the AdS bulk, including whatever is inside the black hole—but, and this is crucial, the information about what’s inside the black hole will be pseudorandomly scrambled. In other words, it works like this: whatever simple thing you’d like to know about parts of the bulk that aren’t hidden behind event horizons—is there a star over here? some gravitational lensing over there? etc.—it seems that you could not only learn it by measuring |ψ⟩, but learn it in polynomial time, the dictionary between bulk and boundary being computationally efficient in that case. (As with almost everything else in this subject, even that hasn’t been rigorously proven, though my postdoc Jason Pollack and I made some progress this past spring by proving a piece of it.) On the other hand, as soon as you want to know what’s inside an event horizon, the fact that there are no probes that an “observer at infinity” could apply to find out, seems to translate into the requisite measurements on |ψ⟩ being exponentially complex to apply. (Technically, you’d have to measure an ensemble of poly(n) identical copies of |ψ⟩, but I’ll ignore that in what follows.)

In more detail, the relevant part of |ψ⟩ turns into a pseudorandom, scrambled mess: a mess that it’s plausible that no polynomial-size quantum circuit could even distinguish from the maximally mixed state. So, while in principle the information is all there in |ψ⟩, getting it out seems as hard as various well-known problems in symmetric-key cryptography, if not literally NP-hard. This is way beyond what we expect even a quantum computer to be able to do efficiently: indeed, after 30 years of quantum algorithms research, the best quantum speedup we know for this sort of task is typically just the quadratic speedup from Grover’s algorithm.

So now you understand why there was some hope that Alice, by jumping into a black hole, could solve a problem that’s exponentially hard for quantum computers! Namely because, once she’s inside the black hole, she can just see the shockwaves, or the volume of the wormhole, or whatever, and no longer faces the exponentially hard task of decoding that information from |ψ⟩. It’s as if the black hole has solved the problem for her, by physically instantiating the otherwise exponentially complex transformation between the bulk and boundary descriptions of |ψ⟩.

Having now gotten your hopes up, the next step in the story is to destroy them.

Here’s the fundamental problem: |ψ⟩ does not represent the CFT dual of a bulk universe that contains the black hole with the shockwaves or whatever, and that also contains Alice herself, floating outside the black hole, and being given |ψ⟩ as an input.  Indeed, it’s unclear what the latter state would even mean: how do we get around the circularity in its definition? How do we avoid an infinite regress, where |ψ⟩ would have to encode a copy of |ψ⟩ which would have to encode a copy of … and so on forever? Furthermore, who created this |ψ⟩ to give to Alice? We don’t normally imagine that an “input state” contains a complete description of the body and brain of the person whose job it is to learn the output.

By contrast, a scenario that we can define without circularity is this: Alice is given (via physical qubits, a giant table of amplitudes, an obfuscated quantum circuit, or whatever) a pure quantum state |ψ⟩, which represents the CFT dual of a hypothetical universe containing a black hole.  Alice wants to learn what shockwaves or wormholes are inside the black hole, a problem plausibly conjectured not to have any ordinary polynomial-size quantum circuit that takes copies of |ψ⟩ as input.  To “solve” the problem, Alice sets into motion the following sequence of events:

1. Alice scans and uploads her own brain into a quantum computer, presumably destroying the original meat brain in the process! The QC represents Alice, who now exists only virtually, via a state |φ⟩.
2. The QC performs entangling operations on |φ⟩ and |ψ⟩, which correspond to inserting Alice into the bulk of the universe described by |ψ⟩, and then having her fall into the black hole.
3. Now in simulated form, “Alice” (or so we assume, depending on our philosophical position) has the subjective experience of falling into the black hole and observing what’s inside.  Success! Given |ψ⟩ as input, we’ve now caused “Alice” (for some definition of “Alice”) to have observed the answer to the beyond-BQP computational problem.

In the panel discussion, I now model Susskind as having proposed scenario 1-3, Witten as going along with 1-2 but rejecting 3 or not wanting to discuss it, and me as having made valid points about the computational complexity of simulating Alice’s experience in 1-3, yet while being radically mistaken about what the scenario was (I still thought an actual black hole was involved).

An obvious question is whether, having learned the answer, “Alice” can now get the answer back out to the “real, original” world. Alas, the expectation is that this would require exponential time. Why? Because otherwise, this whole process would’ve constituted a subexponential-time algorithm for distinguishing random from pseudorandom states using an “ordinary” quantum computer! Which is conjectured not to exist.

And what about Alice herself? In polynomial time, could she return from “the Matrix,” back to a real-world biological body? Sure she could, in principle—if, for example, the entire quantum computation were run in reverse. But notice that reversing the computation would also make Alice forget the answer to the problem! Which is not at all a coincidence: if the problem is outside BQP, then in general, Alice can know the answer only while she’s “inside the Matrix.”

Now that hopefully everything is crystal-clear and we’re all on the same page, what can we say about this scenario?  In particular: should it cause us to reject or modify the QECTT itself?

Daniel Gottesman, I thought, offered a brilliant reductio ad absurdum of the view that the simulated black hole scenario should count as a refutation of the QECTT. Well, he didn’t call it a “reductio,” but I will.

For the reductio, let’s forget not only about quantum gravity but even about quantum mechanics itself, and go all the way back to classical computer science.  A fully homomorphic encryption scheme, the first example of which was discovered by Craig Gentry 15 years ago, lets you do arbitrary computations on encrypted data without ever needing to decrypt it.  It has both an encryption key, for encrypting the original plaintext data, and a separate decryption key, for decrypting the final answer.

Now suppose Alice has some homomorphically encrypted top-secret emails, which she’d like to read.  She has the encryption key (which is public), but not the decryption key.

If the homomorphic encryption scheme is secure against quantum computers—as the schemes discovered by Gentry and later researchers currently appear to be—and if the QECTT is true, then Alice’s goal is obviously infeasible: decrypting the data will take her exponential time.

Now, however, a classical version of Lenny comes along, and explains to Alice that she simply needs to do the following:

1. Upload her own brain state into a classical computer, destroying the “meat” version in the process (who needed it?).
2. Using the known encryption key, homomorphically encrypt a computer program that simulates (and thereby, we presume, enacts) Alice’s consciousness.
3. Using the homomorphically encrypted Alice-brain, together with the homomorphically encrypted input data, do the homomorphic computations that simulate the process of Alice’s brain reading the top-secret emails.

The claim would now be that, inside the homomorphic encryption, the simulated Alice has the subjective experience of reading the emails in the clear.  Aha, therefore she “broke” the homomorphic encryption scheme! Therefore, assuming that the scheme was secure even against quantum computers, the QECTT must be false!

According to Gottesman, this is almost perfectly analogous to Lenny’s black hole scenario.  In particular, they share the property that “encryption is easy but decryption is hard.”   Once she’s uploaded her brain, Alice can efficiently enter the homomorphically encrypted world to see the solution to a hard problem, just like she can efficiently enter the black hole world to do the same.  In both cases, however, getting back to her normal world with the answer would then take Alice exponential time.  Note that in the latter case, the difficulty is not so much about “escaping from a black hole,” as it is about inverting the AdS/CFT dictionary.

Going further, we can regard the AdS/CFT dictionary as, itself, an example of a fully homomorphic encryption scheme—in this case, of course, one where the ciphertexts are quantum states.  This strikes me as potentially an important insight about AdS/CFT itself, even if that wasn’t Gottesman’s intention. It complements many other recent connections between AdS/CFT and theoretical computer science, including the view of AdS/CFT as a quantum error-correcting code, and the connection between AdS/CFT and the Max-Flow/Min-Cut Theorem (see also my talk about my work with Jason Pollack).

So where’s the reductio?  Well, when it’s put so starkly, I suspect that not many would regard Gottesman’s classical homomorphic encryption scenario as a “real” challenge to the QECTT.  Or rather, people might say: yes, this raises fascinating questions for the philosophy of mind, but at any rate, we’re no longer talking about physics.  Unlike with (say) quantum computing, no new physical phenomenon is being brought to light that lets an otherwise intractable computational problem be solved.  Instead, it’s all about the user herself, about Alice, and which physical systems get to count as instantiating her.

It’s like, imagine Alice at the computer store, weighing which laptop to buy. Besides weight, battery life, and price, she definitely does care about processing power. She might even consider a quantum computer, if one is available. Maybe even a computer with a black hole, wormhole, or closed timelike curve inside: as long as it gives the answers she wants, what does she care about the innards? But a computer whose normal functioning would (pessimistically) kill her or (optimistically) radically change her own nature, trapping her in a simulated universe that she can escape only by forgetting the computer’s output? Yeah, I don’t envy the computer salesman.

Anyway, if we’re going to say this about the homomorphic encryption scenario, then shouldn’t we say the same about the simulated black hole scenario?  Again, from an “external” perspective, all that’s happening is a giant BQP computation.  Anything beyond BQP that we consider to be happening, depends on adopting the standpoint of an observer who “jumps into the homomorphic encryption on the CFT boundary”—at which point, it would seem, we’re no longer talking about physics but about philosophy of mind.

So, that was the story! I promised you that it would integrally involve black holes, holography, the Quantum Extended Church-Turing Thesis, fully homomorphic encryption, and brain uploading, and I hope to have delivered on my promise.

Of course, while this blog post has forever cleared up all philosophical confusions about AdS/CFT and the Quantum Extended Church-Turing Thesis, many questions of a more technical nature remain open. For example: what about the original scenario? can we argue that the experiences of bulk observers can be simulated in BQP, even when those observers jump into black holes? Also, what can we say about the complexity class of problems to which the simulated Alice can learn the answers? Could she even solve NP-complete problems in polynomial time this way, or at least invert one-way functions? More broadly, what’s the power of “BQP with an oracle for applying the AdS/CFT dictionary”—once or multiple times, in one direction or both directions?

Lenny himself described his gedankenexperiment as exploring the power of a new complexity class that he called “JI/poly,” where the JI stands for “Jumping In” (to a black hole, that is). The nomenclature is transparently ridiculous—“/poly” means “with polynomial-size advice,” which we’re not talking about here—and I’ve argued in this post that the “JI” is rather misleading as well. If Alice is “jumping” anywhere, it’s not into a black hole per se, but into a quantum computer that simulates a CFT that’s dual to a bulk universe containing a black hole.

In a broader sense, though, to contemplate these questions at all is clearly to “jump in” to … something. It’s old hat by now that one can start in physics and end up in philosophy: what else is the quantum measurement problem, or the Boltzmann brain problem, or anthropic cosmological puzzles like whether (all else equal) we’re a hundred times as likely to find ourselves in a universe with a hundred times as many observers? More recently, it’s also become commonplace that one can start in physics and end in computational complexity theory: quantum computing itself is the example par excellence, but over the past decade, the Harlow-Hayden argument about decoding Hawking radiation and the complexity = action proposal have made clear that it can happen even in quantum gravity.

Lenny’s new gedankenexperiment, however, is the first case I’ve seen where you start out in physics, and end up embroiled in some of the hardest questions of philosophy of mind and computational complexity theory simultaneously.