A Closer Look Into The Microsoft-Atom Computing Logical Qubit Study

Insider Brief

• Microsoft and Atom Computing have demonstrated significant progress in transitioning from physical to logical qubits using a neutral atom quantum processor, showcasing robust error correction and advanced computational capabilities.
• The study used ytterbium atoms in a programmable grid to entangle 24 logical qubits and perform computations on 28 logical qubits, demonstrating reduced error rates through advanced error-correction techniques.
• The collaboration highlights the possibilities of integrating advanced error-correction software with scalable hardware, building a platform development for fault-tolerant quantum computing.

Transitioning quantum computation from physical to logical qubits is emerging as a critical step in addressing the field’s biggest hurdle — errors. By now, news has circulated throughout the scientific community that Microsoft Azure Quantum and Atom Computing researchers were able to entangle the largest number of logical qubits achieved to date.

Now that the team has published its study on the preprint server ArXiv, which walks the reader through how they used a neutral atom quantum processor with 256 qubits to create and manipulate 24 logical qubits. They have also demonstrated the ability to detect and correct errors and perform computation, on 28 logical qubits, according to a blog post earlier this week.

By encoding information across multiple physical qubits, the scientists achieved error rates significantly lower than those of physical qubits alone, marking what most experts agree is a critical advance toward scalable, fault-tolerant quantum computing.

While the headline logical qubits work is newsworthy enough, there are actually more important details that bubble below the surface of the research. For example, the findings highlight the growing viability of neutral atom platforms, which the researchers suggest could serve as a path toward scientific quantum advantage, where quantum computers can outperform classical machines on specific tasks. The study’s results also includes insights into reliable error detection, algorithm implementation and fault-tolerant computation, all critical to realizing the promise of quantum computing. The Microsoft-Atom Computing partnership, itself, shows how Microsoft is leveraging its global leadership in software and platform development to help move quantum from lab to living room.

In this piece, we’ll look at the findings, the methods, implications and — because no scientific advance is without an assortment of accompanying challenges — we’ll discuss limitations of the study. Those limitations typically form a plan for future work, so we will review some ideas about future directions. Because the study is highly technical, when possible, I’ll try to explain some of the scientific terms, aspects and nomenclature that might be unfamiliar to non-technical writers.

From Physical to Logical Qubits

At the heart of this research is the distinction between physical and logical qubits. It may not sound like a big deal, but it is. Physical qubits are the building blocks of quantum processors, but they are notoriously prone to errors caused by environmental noise, imperfections in hardware, and the fragility of quantum states. These errors make it difficult to scale quantum computations; even the best physical qubits can only execute a limited number of operations before their results become unreliable.

Logical qubits, by contrast, distribute quantum information across a bunch of those physical qubits using error-correcting codes. This redundancy allows errors to be detected and corrected, substantially reducing the effective error rate. It might be a stretch, but you could consider physical qubits as lights in a chandelier. They might flicker, or suddenly go out, but the chandelier itself — the logical qubit in this scenario — will shine steadily because its lit by the combined light of the other bulbs.

While logical qubits require more physical resources, they are indispensable for achieving fault-tolerant quantum computing — the ability to run complex algorithms reliably over long periods.

Methods and Innovations

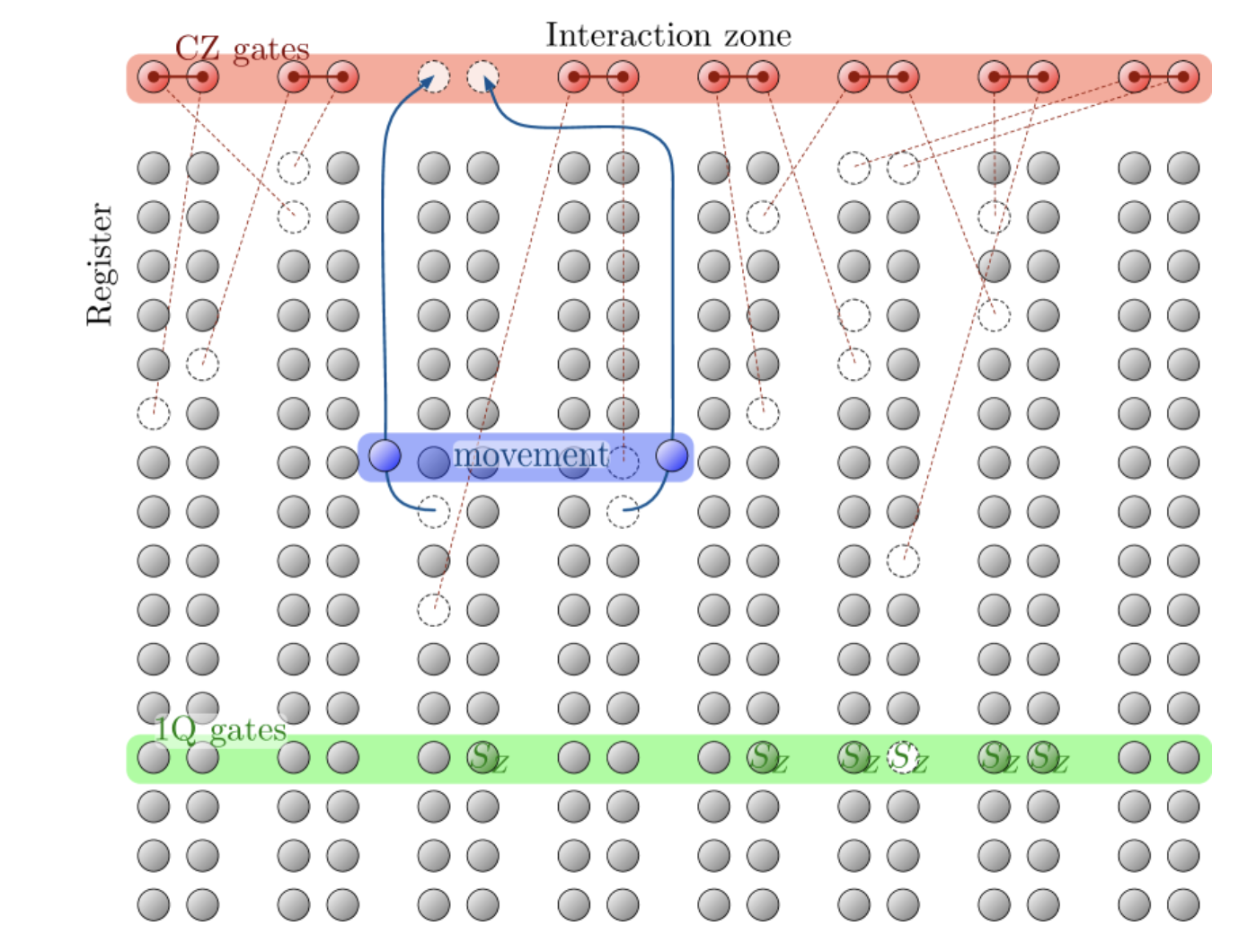
In this study, researchers used a neutral atom quantum processor to encode logical qubits with error-correcting codes. Neutral atom systems use laser beams to trap and manipulate individual atoms, typically of elements like ytterbium or rubidium, arranging them in programmable grids where their quantum states can be controlled and entangled for computation.

The neutral atom platform in this study relied ytterbium atoms — which are noted in the literature as facilitating high-fidelity operations and robust error correction — as qubits. These atoms are trapped and manipulated using laser beams in a programmable grid. The platform’s key advantage lies in its scalability and flexibility: atoms can be moved to enable all-to-all connectivity, which means every qubit in a quantum computer can directly interact with every other qubit. This feature is critical for implementing complex quantum circuits.

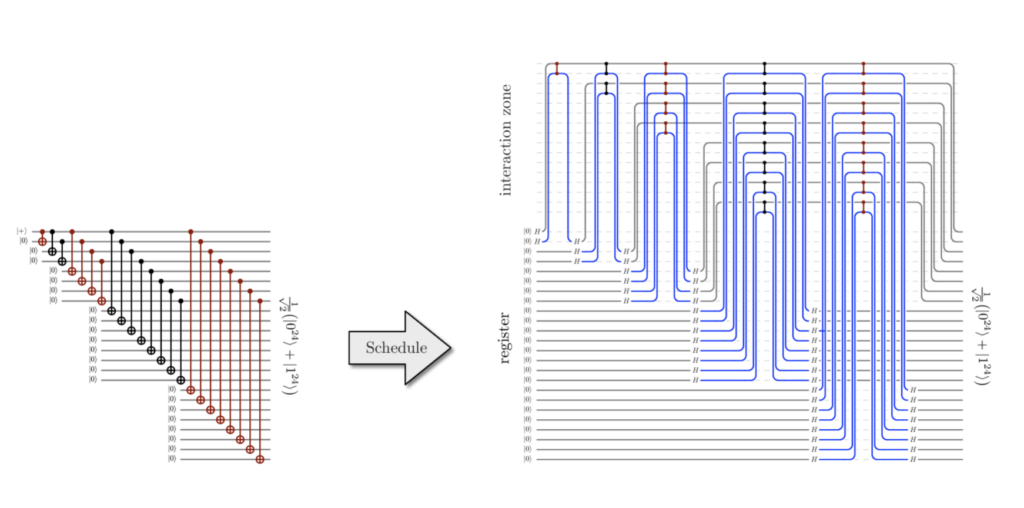
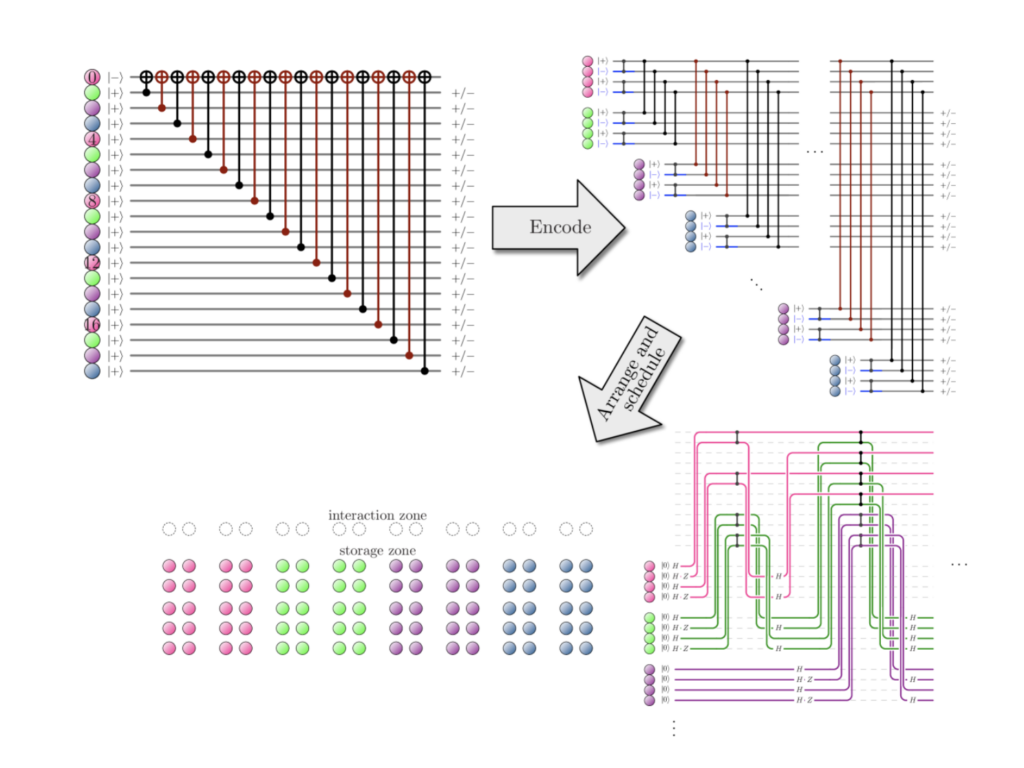
The researchers relied on two primary error-correcting codes: the ⟦4,2,2⟧ code and the ⟦9,1,3⟧ Bacon-Shor code. The ⟦4,2,2⟧ code allowed the team to entangle 24 logical qubits, forming what is known as a “cat” state—a highly entangled quantum state that serves as a benchmark for hardware performance. Meanwhile, the ⟦9,1,3⟧ code was used to demonstrate the correction of both qubit loss and logical errors, a significant step toward practical quantum error correction.

If you’re like me, you are filled with anxiety anytime you see things like brackets with numbers in them and, in general, any form of scientific notation in text. But it’s pretty simple to break this down, even if you’re not a quantum scientists. This is nothing more than a code in a three-number format, we’ll call it ⟦n, k, d⟧, which summarizes structure and purpose. The first number, n, represents the total number of physical qubits—the building blocks of a quantum computer—required to implement the code. The second, k, is the number of logical qubits encoded within those physical qubits. Logical qubits are those error-protected units that form the foundation of reliable quantum computations. The final number, d, stands for the code’s “distance,” or the minimum number of physical qubits that must be corrupted to disrupt the encoded logical information. A higher distance means the code is better at detecting and correcting errors.

In the study, then, researchers employed two codes: the ⟦4,2,2⟧ and ⟦9,1,3⟧ codes. The ⟦4,2,2⟧ code encodes two logical qubits within four physical qubits, offering a balance between efficiency and basic error protection. It is particularly effective at correcting qubit loss, which is when a physical qubit drops out of a computation. This code allowed the team to entangle 24 logical qubits into a “cat” state — or that benchmark entangled state that demonstrates hardware performance.

The ⟦9,1,3⟧ code, by contrast, uses nine physical qubits to encode a single logical qubit, sacrificing efficiency for stronger error correction. With its higher distance, it can address both qubit loss and logical errors, making it ideal for more robust and complex quantum computations.

Overall, what these codes demonstrate these error-correcting methods.

Bernstein-Vazirani Algorithm

One of the study’s key achievements was the implementation of the Bernstein-Vazirani algorithm, a quantum algorithm designed to uncover a hidden binary string using a single quantum query. Classical methods require multiple queries to complete the task. The algorithm is used primarily when scientists want to test the advantage of quantum computing in solving specific types of problems, and its principles contribute to foundational studies in quantum algorithm development and cryptographic applications.

By encoding the algorithm into 28 logical qubits, the Microsoft-Atom Computing team achieved better-than-physical error rates, which shows the robustness of their approach.

Another crucial innovation was the use of a qubit virtualization system, which integrates error correction protocols with the neutral atom processor’s hardware, the paper indicates. This system enabled researchers to detect and correct errors in real time during computations, rather than solely at the end of a circuit. The ability to perform repeated error correction mid-computation is essential for scaling quantum processors to larger and more complex tasks.

Limitations

As is the case with almost every scientific endeavor, the study revealed some challenges still facing quantum error correction and offered ideas for future research. For instance, the error-correcting codes used were relatively low in distance, meaning they could only correct a limited range of errors. Higher-distance codes, which require more physical qubits, will be necessary for fully robust error correction.

Atom movement, while enabling all-to-all connectivity, introduces additional sources of error, such as heating. These errors must be mitigated to improve gate fidelity and ensure the reliability of deeper quantum circuits. Practical factors like laser control precision might be another concern.

The study’s computational depth was also constrained by the current limits of two-qubit gate fidelity and error correction efficiency. Scaling up to larger and more complex algorithms will require improvements in these areas.

Future Directions

Looking ahead, the researchers outlined several areas for improvement, some of which are based on those study limitations. Scaling up to thousands of qubits will enable the use of higher-distance error-correcting codes, reducing the effective error rate even further. Enhancements in two-qubit gate fidelity and noise reduction will allow for deeper and more complex quantum circuits.

The incorporation of mid-circuit measurement and qubit reinitialization could significantly extend the depth of computations by enabling error correction at multiple stages. Additionally, combining these techniques with continuous atom reloading and advanced cooling methods could address fundamental limitations in neutral atom platforms.

Broader Implications

Despite the challenges ahead, the Microsoft-Atom Computing work has been generally acknowledged by quantum computing experts as a meaningful step into a future where quantum systems can tackle more practical problems and engage in calculations that will yield real world — and commercial — benefits.

Specifically, the transition from physical to logical qubits represents a turning point in quantum computing. By achieving error rates lower than those of physical qubits, logical qubits enable the reliable execution of deeper circuits and more complex algorithms. This capability is essential for reaching quantum advantage, where quantum computers can solve problems faster or more accurately than classical machines.

Neutral atom processors are particularly promising for this transition, the study suggests. Their scalability and configurability make them well-suited for implementing advanced error-correcting codes, which can achieve high encoding efficiency with fewer physical qubits. This study positions neutral atoms as a competitive platform alongside superconducting and trapped-ion processors, both of which have also demonstrated progress in logical qubit development.

In a commercial quantum enterprise sense, this work offers insights into Microsoft’s strength as a platform and software company and points to how that company will leverage its expertise to develop the quantum ecosystem, particularly in the industry’s quest to develop robust error-correction protocols, seamless hardware-software integration and cloud-based quantum infrastructure.

If you’re interested in learning even more about this work — and gain a glimpse into the future of logical quantum computing — register for an upcoming joint Microsft-Atom Computing webinar in January.